What is resistance?

BGCSE: Physics

Introduction

Resistance is the opposition to the flow of current through a conductor.
Good conductors of electricity have low resistance, while poor conductors have high resistance.
The SI unit of resistance is the Ohm (Ω).
The resistance of an electric device is calculated using the equation:

$$R = \frac{V}{I}$$

where R is the resistance in ohms(Ω), V is the potential difference in volts(V), and I is the current in amperes(A).

Ohm’s Law

Introduction

Ohm’s law states that the current through a conductor is directly proportional to the voltage across it, provided the temperature of the conductor remains constant.
This law means that the more the voltage, the more the current. Additionally, the more the resistance, the less the current.
You can play with the schematic below by adjusting the voltage and resistance to see how they affect the current.

Simple analogy

Think of electricity as water flowing through a pipe:

Voltage (V) is like the water pressure – how hard the water is being pushed.
Current (I) is how much water is flowing – the flow of electricity.
Resistance (R) is like a narrowing in the pipe – it resists the flow of water.

So, if you increase the pressure (voltage), more water (current) flows. But if the pipe is tighter (more resistance), less water flows.

Everyday example

Imagine a torch (flashlight):

The battery provides the voltage (push).
The wires carry the current (flow).
The bulb has resistance – it glows when current flows through it.

If the battery has more voltage, the bulb shines brighter (more current). But if the bulb has too much resistance, it might not shine much at all!

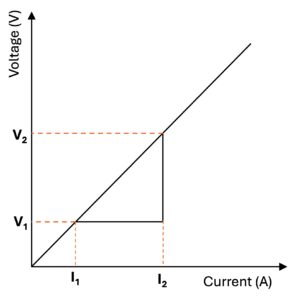
Ohm’s law graph

The graph below shows the relationship between voltage and current as per Ohm’s law. The gradient of graph gives the resistance of the conductor:

$$R = \frac{V_2 – V_1}{I_2 – I_1}$$

Factors affecting the resistance of a conductor (wire)

Length of the wire: The longer the wire, the greater the resistance. The shorter the wire, the less the resistance.
Cross-sectional area: The bigger the cross-sectional area of the wire (or the thicker the wire), the less the resistance and vice versa.
Resistivity of the material: The greater the resistivity of the wire, the greater the resistance and vice versa.
Temperature:
– For metal conductors, the resistance increases as temperature increases.
– For semiconductors, the resistance decreases as temperature increases.

Calculating the resistance of a wire

To calculate the resistance of a wire you need to remember that:

(i) Resistance is directly proportional to the length, L of a wire i.e 𝑅∝L

(ii) Resistance is inversely proportional to the cross-sectional area, 𝐴 of a wire i.e $$R \propto \frac{1}{A}$$

Combining (i) and (ii) we get $$R \propto \frac{L}{A}$$
To make this an equation, we introduce a constant called resistivity to get the equation below:

$$R = \rho \frac{L}{A}$$

Where R is resistance in Ohms (Ω), $$\rho$$ is the resistivity in ohm-meters (Ωm), L is the length in meters (m) and A is the cross-sectional area in square meters (m2)

You adjust the variables below to see how they affect the voltage.

Example 1

A current of 4 A flows through a car headlamp when connected to a 12 V car battery providing a voltage of 12 V across the lamp. Calculate the resistance of the lamp.

Solution

I = 4 A V = 12 V R = ?

$$R = \frac{V}{I}$$

$$R = \frac{12}{4}$$ = 3 Ω

Example 2

Calculate the potential difference required to drive a current of 0.2 A through a torch lamp of resistance 22.5 Ω.

Solution

I = 0.2 A R = 22.5 Ω V = ?

$$R = \frac{V}{I}$$

$$V = I \times R$$

$$V$$ = 0.2 x 22.5 = 4.5 V

Example 3

Silver has a resistivity of 1.6×10-8 Ωm, what would be the resistance of a silver wire of length 0.5m and radius 0.004m?

Solution

ρ = 1.6×10-8 Ωm l = 0.5m r = 0.004m R = ?

$$R = \rho \frac{L}{A}$$

First, we calculate cross cross-sectional area A of the wire as the radius is given:

$$A = \pi \times r^2 = \pi \times 0.004^2 $$ = 5.027 x $$10^{-5}$$ m$$^2$$

$$R = \rho \frac{L}{A} = \frac{1.6 \times 10^{-8} \times 0.5}{5.027 \times 10^{-5}}$$

$$R$$ = 1.6 x 10$$^{-4}$$ Ω